Blog

The recent announcement of the likely discovery of the Higgs Boson from both experiment teams at CERN was framed in terms of the statistical significance of their result; in this case at what they called the five-sigma level. So what does five-sigma mean in relation to the discovery of the Higgs Boson? There are some nice explanations in the press. For example, The Wall Street Journal wrote:

“the five-sigma concept is somewhat counterintuitive. It has to do with a one-in-3.5-million probability. That is not the probability that the Higgs boson doesn’t exist. It is, rather, the inverse: If the particle doesn’t exist, one in 3.5 million is the chance an experiment just like the one announced this week would nevertheless come up with a result appearing to confirm it does exist.”

There are also many examples where the result was misinterpreted and David Spiegelhalter gives an interesting run-down of how well the press did in his Understanding Uncertainty blog.

When scientists talk about sigma levels, they are basically talking about how far their observations are from where they might expect them to be. This distance is measured in units of sigma with 1-sigma observation meaning that they would expect 32% of future observation to be at least as far away as what they have observed. The sigma scale isn’t linear though, 2 sigma means that 4.5% of future observations would be more extreme and 3 sigma puts that at 0.4%.

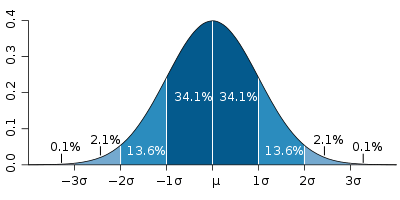
Figure 1: Normal distribution curve that illustrates standard deviations.

In particle physics five-sigma, is the accepted level of significance required to declare a discovery. This corresponds to a probability of 0.00002% which might seem to many to be rather extreme. In fact, for many scientists a two-sigma result would be deemed adequate in order to publicise their results. Why is there a difference?

Essentially the scientists at CERN are risk-averse; the Large Hadron Collider is one of the most publicised and expensive scientific instruments ever built and the scientists involved are not willing to gamble with their scientific reputations or the laws of physics unless there is a very high level of certainty associated with their results. Uncertainties arise; for example, because of the so-called ‘Look Elsewhere Effect’ in that if you do enough tests eventually you’ll get a false positive result. (See, for example our blog linking jelly beans with acne!). The teams at CERN are looking for particles at a range of different energy levels and by taking such extreme sigma levels they reduce the chance of a false positive to scientifically acceptable levels.

What constitutes acceptable levels of uncertainty varies between different fields. In medical statistics, for example, a five-sigma level would not be an ethical choice; there is likely to be a greater benefit to patients in rolling out a new drug quickly than prolonging early trials to ensure a higher level of significance. At the other end of the spectrum, manufacturers often use a six-sigma level as a quality control assurance. The “sigma rating” in a manufacturing process indicates the expected percentage of defect-free products and in a so-called six-sigma process only 3.4 defects per million are expected. As with particle physics, this may seem to be a particularly stringent, but in manufacturing there is a clear relationship between quality and production costs indicating that a high significance level is cost-beneficial. (Note that 3.4 per million actually corresponds to a 4.5 sigma process since an additional 1.5-sigma is included to account for experimental bias.)

The choice of which significance level to use is always a subjective one and conflicts with the scientist or engineer’s intention to conduct an objective test. In most cases, the fundamental question of interest is what is the probability that my hypothesis is true? The only way to do this is to avoid significance testing and sigma-levels altogether and undertake a Bayesian analysis that evaluates precisely that probability.

Related Articles

• Five-sigma – What’s That? (blogs.scientificamerican.com)
• Higgs excitement at fever pitch – BBC News (bbc.co.uk)
• The Particle Proof (blogs.wsj.com)