Meta-analysis: Combining Results from Multiple Studies
In many medical specialties, it is common to find that multiple studies have been conducted to answer similar questions about the effectiveness of a treatment, or the incidence or mortality rates for a particular disease, for example. Meta-analyses are statistical techniques for combining the findings from independent studies and can be used in these cases to determine an overall estimate of the effect or rate of interest.
The Challenge
A doctor carrying out independent research, had performed a literature review of studies reporting the cause-specific mortality rates for a digestive disorder associated with an increased risk of developing cancer as well as other medical complications. Select were asked to bring together the results from these publications in order to produce overall estimates of the various mortality rates, giving due weight to the size of the individual studies included.
The Approach
We combined the information from the independent studies via meta-analyses, modelling the mortality rates as weighted averages of the estimates across the studies. Greater weight was given to the trials with a larger sample size (or equivalently, a lower standard error) as they provide more evidence (or, equivalently, greater certainty) in their estimates. This allowed us to calculate overall estimates of the mortality rates across the studies, along with confidence intervals expressing our uncertainty in those estimates.
Different meta-analysis methods can be applied for different outcome measures when combining summary statistics from multiple studies, but each method uses a similar approach in which the estimate from each study is weighted by the precision of that estimate. As the outcomes of interest were incidence rates in this case (deaths per 1,000 person-years), Poisson regression models were applied to the data.
These approaches can use either a fixed-effects or a random-effects statistical model. A fixed-effects meta-analysis assumes that all of the studies included are estimating the same (fixed) treatment effect, or incidence rate in this case, whereas a random-effects meta-analysis allows for differences in the outcome between studies. A random-effects meta-analysis model assumes that the observed estimates can vary across studies because of real differences in each study as well as sampling variability (i.e., chance). This additional variability may be due to differences in the subjects included in the study, the setting, or the exact definition of the endpoint of interest, and so on.
Heterogeneity tests and measures were used to summarise the amount of variation in the rates between the studies included in the meta-analysis and to assess whether there were differences in the estimates between the studies beyond those expected by chance. These tests were conducted to ensure that the appropriate meta-analysis methods were applied. In this case, random-effects meta-analyses were used due to the statistically significant heterogeneity observed.
Along with summary tables of the results, forest plots were provided to visualize the results of the meta-analyses, showing the mortality rates for each study and the pooled estimates over all of the trials combined, at a glance. An example forest plot is shown in Figure 1. The studies are ordered from top-to-bottom by increasing size of the reported mortality rate.
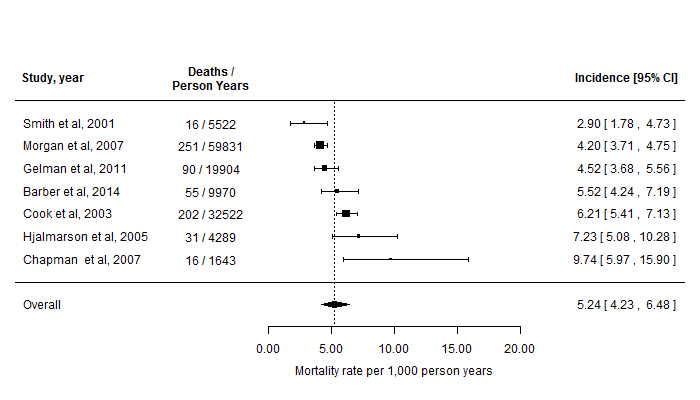
Figure 1: Forest plot showing the reported mortality rates of the studies identified in the literature and the overall rate estimated via a random-effects meta-analysis. Note that for reasons of confidentiality, these data (and study references) have been fabricated for illustration.
It is important to note that the studies included in a meta-analysis should be “combinable” in the sense that together they give clinically meaningful results (as well as having similar endpoints), and should include all relevant studies to synthesize the complete set of evidence available in order to give unbiased results.
The Value
The systematic aggregation of the results from the multiple individual studies helped to give the doctor a clearer picture of the evidence available on the mortality rates for the digestive disorder that they were researching.
A meta-analysis based on a thorough systematic review of the literature, provides a way of combining the evidence to give an unbiased synthesis of the data available. Where the individual studies might contain too few data points to be informative, a meta-analysis can offer more power to detect small but important effects and give more precise estimates of the size of those effects.
Meta-analyses are most often used to assess the effectiveness of healthcare interventions, by combining data from multiple clinical trials. However, a meta-analysis can also be useful in estimating the effect of treatments in many other settings such as agriculture and other industries where chemical interventions are applied, for example, which can help companies to demonstrate the effectiveness of their treatments to their customers.