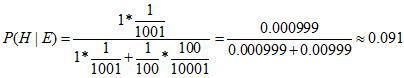The Importance of Probability in Law
The second joint ExIStA and RSS South West Local Group seminar took place on the 11th October with invited speaker Norman Fenton, Director of Risk and Information Management Research at Queen Mary University of London and CEO of Agena Ltd. Norman specialises in quantitative risk assessment covering a wide range of applications including medical trials, financial services and predicting football scores but, for this seminar, he focussed on the fascinating application of law and legal reasoning.
Norman demonstrated that increasingly, forensic evidence in court has a statistical component, but that it is often poorly presented or misunderstood. This can result in fallacies of probabilistic reasoning and ultimately miscarriages of justice. One example is the prosecutor’s fallacy, where prosecutors misuse probabilistic statements about the likelihood of finding a piece of evidence, for example a DNA match, to argue that the probability that the defendant is guilty is high. In reality, the prosecutors are often not taking into account the chance of making a DNA match at random when using a large database of DNA profiles as well as the possibility of errors occurring during the DNA collection and analysis process itself. If the prosecutor were to take these issues into account the reported probability of guilt is often substantially reduced. Norman gave the following simple example during the seminar to illustrate the effect. Suppose we know that the shoe size of the defendant (size 13) matched the size of the criminal’s footprint found at the crime scene. Since size 13 is found nationally in about 1 in 100 men, a common fallacy would be to assume that this means the probability of the defendant being innocent is 1 in 100 (or the probability that he is guilty is 99 in 100). Crucially, we must also take into account the number of other men present at the scene of the crime and the likelihood that they have a shoe size 13. In this example, 1000 others were found to be present at the scene of which 10 also had size 13 shoes. Taking this into consideration, the probability of the defendant’s guilt reduces from 99% to 9% – a very large difference (see the footnote below to understand the mathematics behind this).
To interpret these probabilistic statements correctly, Norman introduced the concept of using Bayesian statistics and, in particular Bayesian networks. These tools allow lawyers to combine information from expert witnesses and forensic evidence and to determine the overall probative value of the evidence. Of course, introducing these tools into the courtroom is not simple and there are still many barriers to overcome including, for example, the complexity of court cases and ensuring the barristers, judges and, not least, the jury fully understand the probabilistic reasoning.
This was a fascinating seminar that gave the audience a glimpse into how important the correct use of probability is in the law to help avoid major miscarriages of justice. Norman used a number of high profile court cases (such as Sally Clark, Stephen Lawrence, Levi Bellfield and Barry George) to demonstrate that the types of fallacies he described are common and to explain how statisticians can help overcome them. Judging by the number of questions and discussion after the talk, it was certainly a great success with the audience! If you’d like to find out more about this topic, we’d recommend Norman’s blog. A video of the seminar itself is also available here.
The probability that the defendant is guilty given the evidence (P(H|E)) is calculated using Bayes Theorem:
We know that without any evidence, the probability of guilt (P(H)) is 1 in 1001 (for there were 1001 people present at the crime scene) and that the probability of finding the evidence of the matching size 13 shoes given the defendant is innocent is 1 in 100 (for size 13 shoes are found in 1 in 100 men). Including this information in the equation, we calculate P(H|E) as follows:
