Why Use a Complex Sample for Your Survey?
What is a complex sample?
Most statistical analyses assume that the data collected are from a simple random sample (SRS) of the population of interest. So say, for example, that you were conducting a survey of employees in your workplace (this is the “population”), a simple random sample would be where each of your colleagues in the office (or “sampling units”) were equally likely to be sampled. However, it’s not always possible or practical to take a simple random sample. Simple random sampling requires access to the whole population of interest (a “complete sampling frame” listing the sampling units) which may not be feasible for large populations. If sampling units are widely spread out geographically, for example, it might also be prohibitively expensive to access and sample across the whole area. Or, if some members of the population (e.g., of a particular demographic background) are relatively low in number, a simple random sample might not obtain enough (or any) of these individuals to reliably measure their responses. So, even if a complete sampling frame is available, it might be much cheaper or more efficient to use a complex sampling scheme instead of SRS, such as multi-stage sampling, clustering and/or stratification, for example.
With these approaches, members of the population don’t all have the same probability of being selected into the sample. Complex samples are most often used for surveys, especially large national or multinational ones where simple random sampling is simply not practical. For example, suppose you were conducting a survey in a conflict-affected country and the target population was all adults aged over 18, totaling, say, 20 million individuals. You might be interested in how responses differ by occupation, but some categories (perhaps self-employed) may only represent a small fraction of the population. You might therefore consider stratifying your sampling to ensure that sufficient responses were obtained to make reliable estimates in each occupation group. The country may also be split geographically into, say, 40 states. To travel to and interview people in each of these states would likely be unfeasible, so cluster sampling might be used so that only a subset of the states needed to be accessed.
Remember – complex samples require statistical methods that take the sampling design into account.
Complex samples may also be incorporated into the design of cross-sectional observational studies or even interventional studies (such as clinical trials). The key thing to remember is that when analysing data from a survey using complex sampling, the statistical methods that you use must take the sampling design into account.
So, what are the most common complex sampling approaches and why and when are they used? We focus here on cluster sampling and stratified sampling. We’ll also discuss sampling without replacement which should also be taken into account when analysing your data.
Clustering
In cluster sampling, the population is split into similar groups of individuals (“clusters”) and then a sample of these clusters is taken (the clusters are the sampling units in this case) so that all of the elements in the selected clusters are included in the sample. Clustering is appropriate when we expect elements in different clusters to be relatively similar (“homogeneous”), i.e., each cluster is representative of the population.
For example, suppose we wanted to gather the opinions of school children in a particular county in England, say Somerset. It would be difficult and expensive to interview all school-aged children in Somerset, so we take a sample of those children instead. However, taking a simple random sample of pupils in Somerset may mean that we still need to survey pupils in all, or a large proportion, of the schools in the county. It would be much cheaper to only survey the pupils in a subset of schools – so, we might cluster pupils according to their schools and then take a sample of the clusters (surveying all students within those selected clusters) to obtain a clustered sample of school children in the county.
This method is most efficient when most of the variation in the population is within clusters, rather than between them (higher within-cluster correlation increases the variance compared to SRS). Cluster sampling is generally used to reduce costs, by reducing the number of clusters that we sample within whilst maintaining the sample efficiency.
Stratification
Stratified sampling
Stratified sampling involves splitting the members of the population into subgroups (“strata”) before sampling, and then applying sampling (usually SRS) separately within each and every group (“stratum”). This is in contrast to cluster sampling where whole clusters are sampled, rather than samples of individuals being taken within each group (i.e., stratum), as illustrated in Figure 1. Stratified sampling can help to ensure that the sample collected is representative of the population, by guaranteeing that sufficient individuals from each sub-group (e.g., gender, or socioeconomic status) will be sampled. This is especially important if some strata only represent a small proportion of the overall population and if the survey responses are expected to differ across the subgroups. For example, responses to a survey might differ by nationality so if we were to miss some of the nationalities in our sample, our results might be biased.
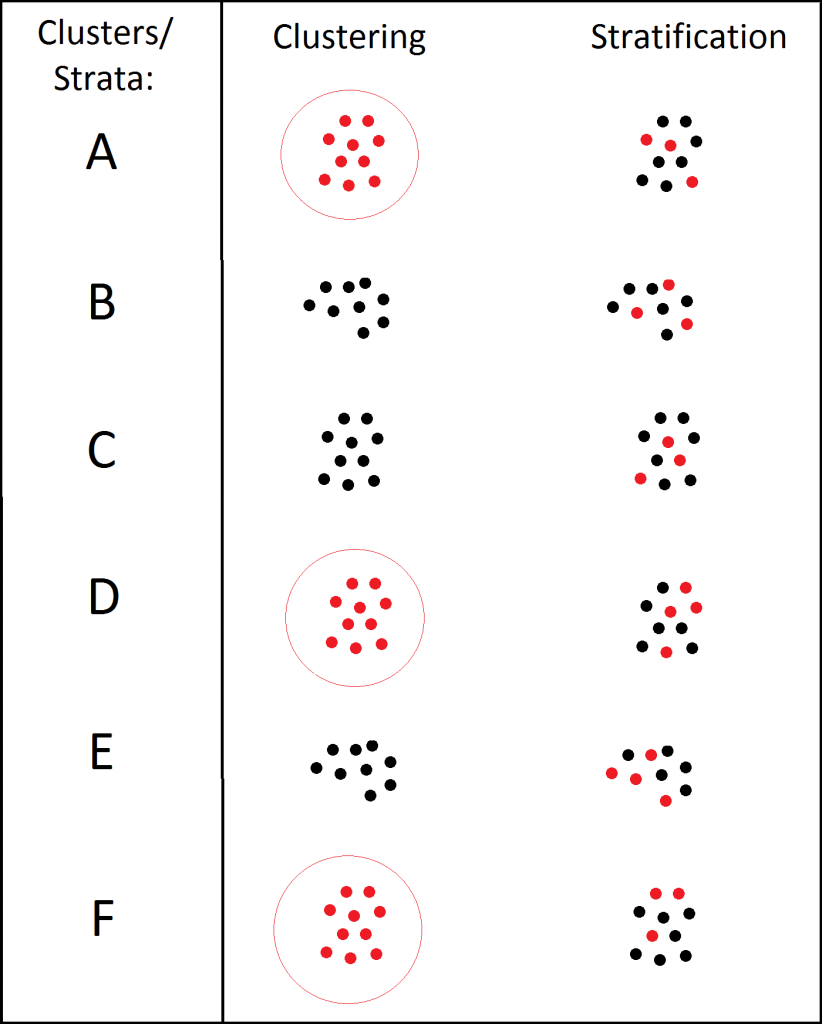
Figure 1: An illustration of clustering (all units within a sample of groups are taken) versus stratified sampling (a sample of units within all groups is taken).
Stratified sampling is appropriate when elements in different clusters are relatively dissimilar (“heterogeneous”), whereas cluster sampling is most efficient when the majority of the variation in the population is within clusters.
Returning to the example of surveying school children in Somerset, we might want to estimate the proportion of pupils with different characteristics stratified (i.e., estimated separately) by school type (e.g., academy, faith school, voluntary aided school, etc.). In this case, we could use stratified sampling to ensure that pupils from different school types are adequately represented in our sample. Schools would be split into strata (e.g., by school type: academy, faith school, voluntary aided school, etc.), and then samples of pupils would be taken within each stratum, to ensure that pupils from each school type were adequately represented in the sample. Contrast this with cluster sampling where we would cluster pupils and then take a sample of the clusters (surveying all students within those selected clusters).
Each stratum can be sampled in proportion to the relative size of that sub-group in the total population (“proportionate allocation”) to make the overall sample as representative as possible. Or, larger samples can be obtained in strata with greater variability to minimise the sampling variance (“optimum allocation”), improving the efficiency of the sample overall.
It is also possible to combine stratified sampling with clustered sampling. For example, we might stratify schools by type and then take cluster samples of schools within each stratum. This is an example of a one-stage cluster sampling scheme but further stages of sampling could be also included. In two-stage cluster sampling, for example, after taking the sample of clusters, a sample of elements within each selected cluster is then taken. So, we might only interview a sample of the pupils in each selected school.
Post-stratification
After completing your survey, you might find that the sample you have taken is not representative of the population (for example, 40% of the population might be male, whereas in the sample obtained only 20% might be males and so males are “under-sampled”). In this case post-stratification can be applied. Such differences can be due to non-response or incomplete coverage, which are an inevitable consequence of the fact that we cannot sample everyone in the population nor compel them to respond. If the sample is imbalanced with respect to key factors that are likely to affect the study/survey responses then they can lead to biases in the results. Sampling weights can be calculated to post-stratify the sample (to adjust the sample data after it has been collected) to ensure that the results are representative of the population. For more information on survey weighting and post-stratification, see our case study on the work we did recently with Sport Wales for their School Sport Survey.
Sampling without replacement
Suppose you were taking a sample of animals from the wild, in order to estimate their average weights, for example. Once one animal had been caught and measured, it would then be released back into the wild. It’s possible, in this case, that you might catch and measure the same animal more than once – we call this “sampling with replacement”. With replacement means that once an individual is selected to be in the sample, that individual is placed back in the population to potentially be sampled again. There are two ways to select a sample from the population – with replacement, as in this example, or without replacement. Without replacement means that once an individual is sampled, that individual cannot be sampled again; they are not placed back in the population. This will often occur when a sample is preselected from a sampling frame, i.e., a list of all those in the population who can be sampled. 
Many standard analysis techniques assume that the sample being analysed was obtained from a sample taken with replacement or from an infinite population (when the population is infinite, or extremely large, then there’s little difference between sampling with and without replacement). However, in practice, most simple random samples are actually taken without replacement from a finite population. In this case, the variability of our sample is actually less than expected, and therefore we can apply a finite population correction to account for this greater efficiency in the sampling process. Each sampled individual is always unique and therefore provides ‘new’ information when sampling without replacement, whereas it’s possible when sampling with replacement to have ‘repeated’ information. When sampling without replacement from a finite population, it may be possible to sample all individuals in which case we’ll have no uncertainty in our estimates. The correction only has a noticeable effect when the sampling fraction, i.e., the proportion of the population sampled, is large. A good rule-of-thumb to decide whether you need to apply a finite population correction is if you obtain a sample that makes up more than 5% of the population you should apply the correction. A finite population correction factor (FPC) is calculated, which is then multiplied by the standard error of the estimate. We’ve recently released a series of sample size and confidence interval calculators, some of which include a finite population correction – for more details (including the formula for the FPC) see the calculators on the Resources section of our website.
How to analyse data from a complex sample
The most important thing to understand about complex sampling is that a more sophisticated analysis is needed when analysing the data collected – standard approaches are not necessarily appropriate. We must take account of the sample design in order for our conclusions to be reliable, whether we are estimating a characteristic of the population or testing for effects, for example.
The usual standard errors, assuming a simple random sample with replacement, will be incorrect if a complex sample has been taken. For example, a sample that is collected using cluster sampling underestimates the true population variance. Adjusting the standard errors to account for the complex sampling plan we find that they are larger, if correctly estimated, than those that would have been obtained assuming a simple random sample of the same size. This is because we might expect responses within a cluster to be more similar to each other than for randomly selected individuals across the population. Without correcting for these under-estimates, we increase the risk of falsely determining significant effects when they do not actually exist (“false positives”).
In the statistical software package SPSS, complex samples analysis plans can be generated which, when used alongside the corresponding Analyze>Complex Samples menu, ensure that the sample design is incorporated into the analysis. In R, the survey package similarly allows you to specify a complex survey design and carry out appropriate analyses taking the design into account. Other packages in R, such as the anesrake package are also useful for implementing survey weighting, for example.
Complex samples are a useful tool for creating more efficient (e.g., stratified sampling with optimum allocation) or cheaper (e.g., cluster sampling) sampling designs. However, it’s crucial when using a complex sample to account for the sampling design when analysing your data in order to ensure that the results are accurate and reliable. If you’re conducting a survey using complex sampling and need help with the survey design or analysis, contact us to find out how we can help.
Related Articles
- The Myth of Random Sampling
- Eurostat survey sampling reference guidelines (SSN 1977-0375 Eurostat Methodologies and Working papers)
- Analysis of Complex Sample Survey Data in SAS