Market Basket Analysis: Understanding Customer Behaviour
In a previous blog post, we discussed how supermarkets use data to better understand consumer needs and, ultimately, increase their overall spend. One of the key techniques used by the large retailers is called Market Basket Analysis (MBA), which uncovers associations between products by looking for combinations of products that frequently co-occur in transactions. In other words, it allows the supermarkets to identify relationships between the products that people buy. For example, customers that buy a pencil and paper are likely to buy a rubber or ruler.
“Market Basket Analysis allows retailers to identify relationships between the products that people buy.”
Retailers can use the insights gained from MBA in a number of ways, including:
- Grouping products that co-occur in the design of a store’s layout to increase the chance of cross-selling;
- Driving online recommendation engines (“customers who purchased this product also viewed this product”); and
- Targeting marketing campaigns by sending out promotional coupons to customers for products related to items they recently purchased.
Given how popular and valuable MBA is, we thought we’d produce the following step-by-step guide describing how it works and how you could go about undertaking your own Market Basket Analysis.
How does Market Basket Analysis work?
To carry out an MBA you’ll first need a data set of transactions. Each transaction represents a group of items or products that have been bought together and often referred to as an “itemset”. For example, one itemset might be: {pencil, paper, staples, rubber} in which case all of these items have been bought in a single transaction.
In an MBA, the transactions are analysed to identify rules of association. For example, one rule could be: {pencil, paper} => {rubber}. This means that if a customer has a transaction that contains a pencil and paper, then they are likely to be interested in also buying a rubber.
Before acting on a rule, a retailer needs to know whether there is sufficient evidence to suggest that it will result in a beneficial outcome. We therefore measure the strength of a rule by calculating the following three metrics (note other metrics are available, but these are the three most commonly used):
Support: the percentage of transactions that contain all of the items in an itemset (e.g., pencil, paper and rubber). The higher the support the more frequently the itemset occurs. Rules with a high support are preferred since they are likely to be applicable to a large number of future transactions.
Confidence: the probability that a transaction that contains the items on the left hand side of the rule (in our example, pencil and paper) also contains the item on the right hand side (a rubber). The higher the confidence, the greater the likelihood that the item on the right hand side will be purchased or, in other words, the greater the return rate you can expect for a given rule.
Lift: the probability of all of the items in a rule occurring together (otherwise known as the support) divided by the product of the probabilities of the items on the left and right hand side occurring as if there was no association between them. For example, if pencil, paper and rubber occurred together in 2.5% of all transactions, pencil and paper in 10% of transactions and rubber in 8% of transactions, then the lift would be: 0.025/(0.1*0.08) = 3.125. A lift of more than 1 suggests that the presence of pencil and paper increases the probability that a rubber will also occur in the transaction. Overall, lift summarises the strength of association between the products on the left and right hand side of the rule; the larger the lift the greater the link between the two products.
To perform a Market Basket Analysis and identify potential rules, a data mining algorithm called the ‘Apriori algorithm’ is commonly used, which works in two steps:
- Systematically identify itemsets that occur frequently in the data set with a support greater than a pre-specified threshold.
- Calculate the confidence of all possible rules given the frequent itemsets and keep only those with a confidence greater than a pre-specified threshold.
The thresholds at which to set the support and confidence are user-specified and are likely to vary between transaction data sets. R does have default values, but we recommend that you experiment with these to see how they affect the number of rules returned (more on this below). Finally, although the Apriori algorithm does not use lift to establish rules, you’ll see in the following that we use lift when exploring the rules that the algorithm returns.
Performing Market Basket Analysis in R
To demonstrate how to carry out an MBA we’ve chosen to use R and, in particular, the arules package. For those that are interested we’ve included the R code that we used at the end of this blog.
Here, we follow the same example used in the arulesViz Vignette and use a data set of grocery sales that contains 9,835 individual transactions with 169 items. The first thing we do is have a look at the items in the transactions and, in particular, plot the relative frequency of the 25 most frequent items in Figure 1. This is equivalent to the support of these items where each itemset contains only the single item. This bar plot illustrates the groceries that are frequently bought at this store, and it is notable that the support of even the most frequent items is relatively low (for example, the most frequent item occurs in only around 2.5% of transactions). We use these insights to inform the minimum threshold when running the Apriori algorithm; for example, we know that in order for the algorithm to return a reasonable number of rules we’ll need to set the support threshold at well below 0.025.
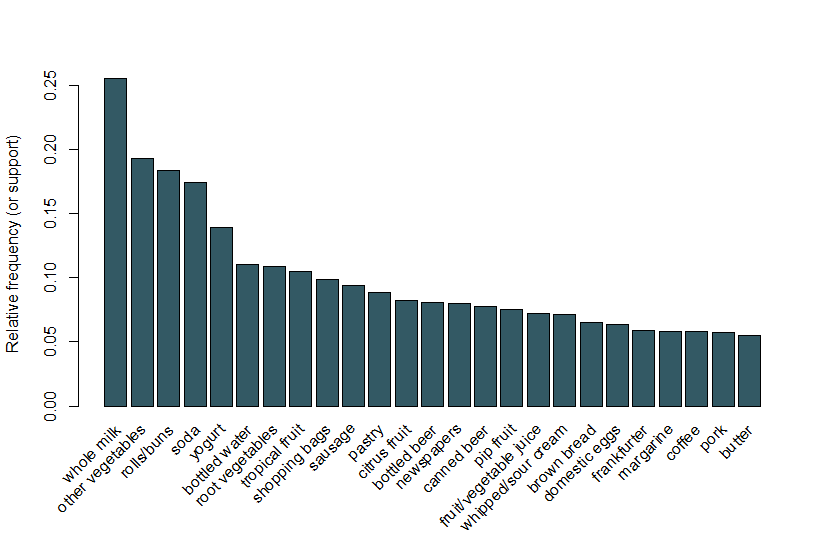
Figure 1 A bar plot of the support of the 25 most frequent items bought.
By setting a support threshold of 0.001 and confidence of 0.5, we can run the Apriori algorithm and obtain a set of 5,668 results. These threshold values are chosen so that the number of rules returned is high, but this number would reduce if we increased either threshold. We would recommend experimenting with these thresholds to obtain the most appropriate values. Whilst there are too many rules to be able to look at them all individually, we can look at the five rules with the largest lift:
| Rule | Support | Confidence | Lift |
| {instant food products,soda}=>{hamburger meat} | 0.001 | 0.632 | 19.00 |
| {soda, popcorn}=>{salty snacks} | 0.001 | 0.632 | 16.70 |
| {flour, baking powder}=>{sugar} | 0.001 | 0.556 | 16.41 |
| {ham, processed cheese}=>{white bread} | 0.002 | 0.633 | 15.05 |
| {whole milk, instant food products}=>{hamburger meat} | 0.002 | 0.500 | 15.04 |
Table 1: The five rules with the largest lift.
These rules seem to make intuitive sense. For example, the first rule might represent the sort of items purchased for a BBQ, the second for a movie night and the third for baking.
Rather than using the thresholds to reduce the rules down to a smaller set, it is usual for a larger set of rules to be returned so that there is a greater chance of generating relevant rules. Alternatively, we can use visualisation techniques to inspect the set of rules returned and identify those that are likely to be useful.
Using the arulesViz package, we plot the rules by confidence, support and lift in Figure 2. This plot illustrates the relationship between the different metrics. It has been shown that the optimal rules are those that lie on what’s known as the “support-confidence boundary”. Essentially, these are the rules that lie on the right hand border of the plot where either support, confidence or both are maximised. The plot function in the arulesViz package has a useful interactive function that allows you to select individual rules (by clicking on the associated data point), which means the rules on the border can be easily identified.
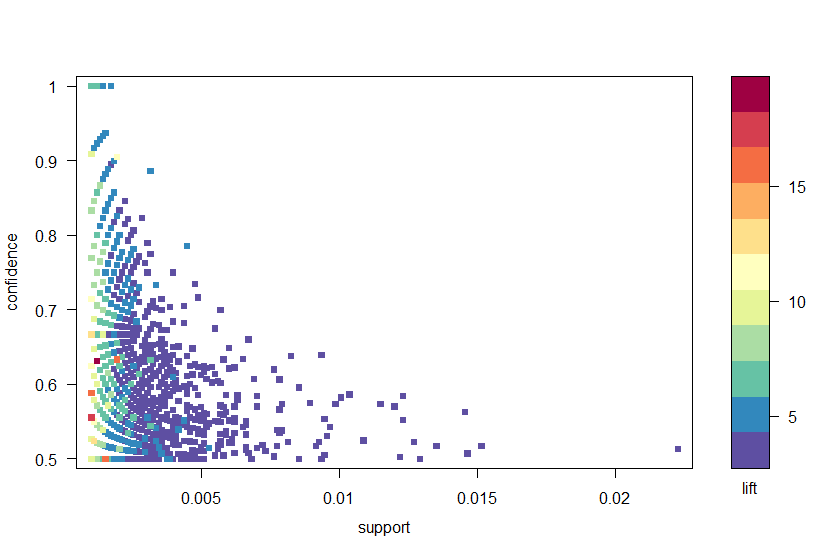
Figure 2: A scatter plot of the confidence, support and lift metrics.
There are lots of other plots available to visualise the rules, but one other figure that we would recommend exploring is the graph-based visualisation (see Figure 3) of the top ten rules in terms of lift (you can include more than ten, but these types of graphs can easily get cluttered). In this graph the items grouped around a circle represent an itemset and the arrows indicate the relationship in rules. For example, one rule is that the purchase of sugar is associated with purchases of flour and baking powder. The size of the circle represents the level of confidence associated with the rule and the colour the level of lift (the larger the circle and the darker the grey the better).
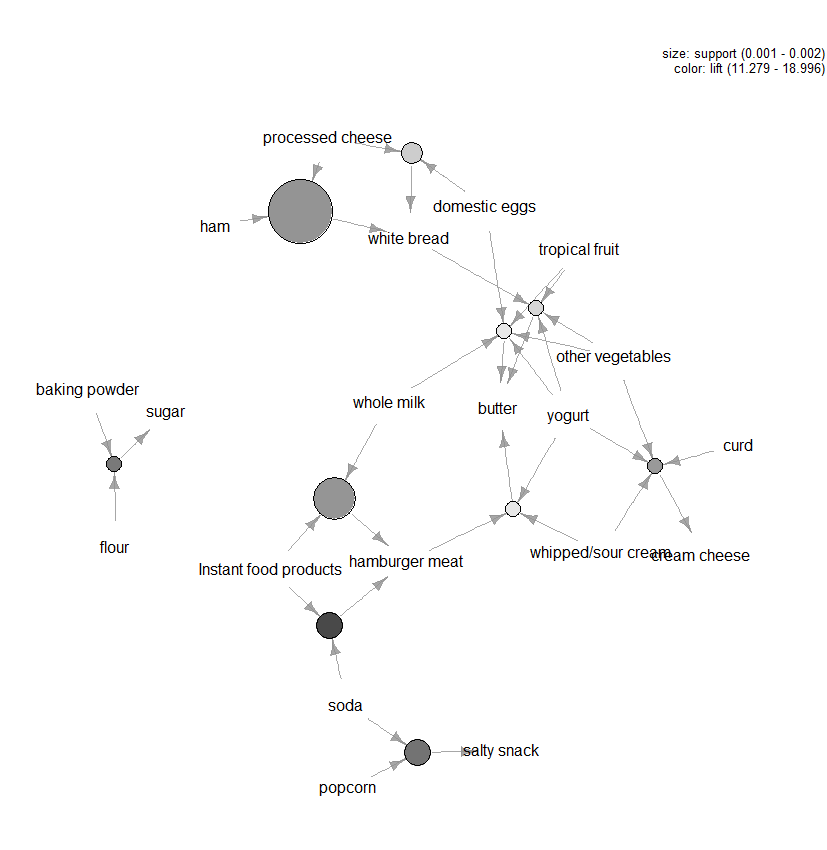
Figure 3: Graph-based visualisation of the top ten rules in terms of lift.
Market Basket Analysis is a useful tool for retailers who want to better understand the relationships between the products that people buy. There are many tools that can be applied when carrying out MBA and the trickiest aspects to the analysis are setting the confidence and support thresholds in the Apriori algorithm and identifying which rules are worth pursuing. Typically the latter is done by measuring the rules in terms of metrics that summarise how interesting they are, using visualisation techniques and also more formal multivariate statistics. Ultimately the key to MBA is to extract value from your transaction data by building up an understanding of the needs of your consumers. This type of information is invaluable if you are interested in marketing activities such as cross-selling or targeted campaigns.
If you’d like to find out more about how to analyse your transaction data, please contact us and we’d be happy to help.
R Code
library("arules")
library("arulesViz")
#Load data set:
data("Groceries")
summary(Groceries)
#Look at data:
inspect(Groceries[1])
LIST(Groceries)[1]
#Calculate rules using apriori algorithm and specifying support and confidence thresholds:
rules = apriori(Groceries, parameter=list(support=0.001, confidence=0.5))
#Inspect the top 5 rules in terms of lift:
inspect(head(sort(rules, by ="lift"),5))
#Plot a frequency plot:
itemFrequencyPlot(Groceries, topN = 25)
#Scatter plot of rules:
library("RColorBrewer")
plot(rules,control=list(col=brewer.pal(11,"Spectral")),main="")
#Rules with high lift typically have low support.
#The most interesting rules reside on the support/confidence border which can be clearly seen in this plot.
#Plot graph-based visualisation:
subrules2 <- head(sort(rules, by="lift"), 10)
plot(subrules2, method="graph",control=list(type="items",main=""))